2015/11/04
- メモリに格納するもしくは、読みだすデータには、そこに厳密性が求められるものとそうでないものがあります。例えば画像データなどは、1bit程度違っていても実使用上その間違いは問題無いかもしれませんが、ネットワークのパケットデータなどはそうもいきません。しかしながらメモリ内のデータはソフトエラーやSEU(Single Event Upset)等の影響により変わってしまうことがあります。この対応の一つとしてECC(Error Correction Code)と呼ばれる仕組みがあります。
- このECC回路はメモリのマクロ内に入っている又はソフトIPとしてRAMの外に置くなど、FPGAもしくはASICのメーカによって思想が異なっています。例えばFPGAのメモリマクロに入っているからという理由で使ってしまうと、ASIC等に横展開する場合、困ったことになる(*1)のは言うまでもありません。
- 今回のレポートでは通常のパリティ検査符号を用いたものと、実質こちらがメインですがハミング符号を用いたECCについて説明したいと思います。尚、説明について行列が云々といった数学の話は一切出しません。
- まずParity検査符号ですが、これは'1'になっているbitが偶数か奇数かを判定するもので、演算としては全bitを排他的論理和(Exclusive OR)した結果です。例えばdata[3:0](4bitです)の場合
data[3:0] = 4'b0110 : Parity検査符号 = 0 (1が偶数)
data[3:0] = 4'b1110 : Parity検査符号 = 1 (1が奇数)
といった結果になります。 - Parity検査符号をVerilog-HDLの論理として書くと
assign parity = data[3] ^ data[2] ^ data[1] ^ data[0]; 又は assign parity = ^data;
のように記述できます。回路のイメージは下記になります。
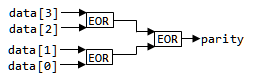
- このParity検査符号を使った16bitデータのECCを考えてみます。下記のように4 x 4の表に16bitのデータを置き、行と列それぞれにParity検査符号を置くのが簡単でしょう。水平垂直Parity検査方式と言われています。
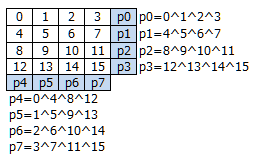
- このとき、例えば5bit目でデータが変わっていたら(反転していたら)、p1(=4^5^6^7)とp5(=1^5^9^13)の2bitのParity検査符号が異なる結果となるため、5bit目のデータを修正すれば良いことがわかります。
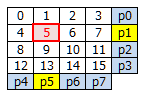
- しかしながらデータエラーが2bit起きると、エラーは検出できても修正すべきbitが特定できません。下図で言えば、赤枠内のどこか2bitというところまでしかわかりません。ここは後述のハミング符号を用いたECCでも同じです。
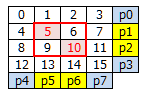
ちなみに、1bitのエラーは訂正可能で、2bitエラーは訂正不能だが検出可能な回路をSECDED(Single-bit Error Correction Double-bit Error Detection)と呼びます。 - さて、これで仕組みとしてはECCが可能なわけですが、実際Parity 8bitを含むワードのデータは「16+8=24bit」になります。1/3がParityデータというのはちょっと大きいですね...。

これはメモリの容量を消費してしまうことも問題(*2)ですが、そもそもECC用のParityデータが大きいと、Parityデータ自身の壊れる確率が上がり、耐障害という観点では意味が無くなってしまいます。つまりできるだけECC用のParityデータは小さくしたいわけです。
- Parity検査データの組み合わせで、16bitデータのどこがおかしいか指し示すことを考えた場合、「16bit:0〜15」それぞれを表すには「4bit」の検査データが必要です。ただし「4'b0000」は「問題無し」の意味になってしまうので「1〜16」として考えるとすれば「5bit」の検査データが必要になります。
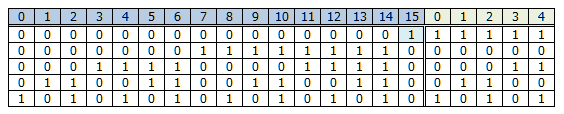
- この考え方に従い、16bitのデータ本体と、5bitのParity検査データ相当分を合わせた21bitのデータについて「5'b00001」から順番に割り当てていったのが以下の表です。ここではまだ何も考えていません。ただ順番に割り当てただけです。
-
上記の表を列方向に見た時「1」が「1bitだけ立っている」ところを黄色背景にしてみました。元の番号で「0,1,3,7,15」に相当する5列です。そこに改めて番号を0〜4(緑背景)で振り直し、それ以外の列にも左から順番に番号を0〜15で振り直し(青背景)たのが2行めです。
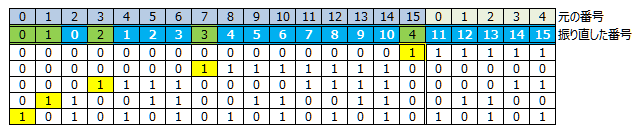
- もう少し見やすくするため、「1」が「1bitだけ立っている」列を左に寄せたのが、下記表になります。この表は緑背景列0〜4がParity検査bit、青背景0〜15が16bitのデータ本体を意味しています。データ本体の「1」は赤背景にしました。
表.SEC符号表

-
例えば表の2行めを見ると、データの11〜15に「1」が置かれていますが、これは5bitのParity検査符号の一つに対し
[11]^[12]^[13]^[14]^[15]
を与えることを意味しています。[*]はデータ番号*の中身を表しています。 - これと同様に、5bitのParity検査式を上記表を参照して書くと下記になります。一応式にしてみたものの、どう見ても表のほうがわかりやすいですね。
Parity[4]=[11]^[12]^[13]^[14]^[15]
Parity[3]=[4]^[5]^[6]^[7]^[8]^[9]^[10]
Parity[2]=[1]^[2]^[3]^[7]^[8]^[9]^[10]^[14]^[15]
Parity[1]=[0]^[2]^[3]^[5]^[6]^[9]^[10]^[12]^[13]
Parity[0]=[0]^[1]^[3]^[4]^[6]^[8]^[10]^[11]^[13]^[15] -
しかし、これだとまだ少し足りません。仮にデータの「2bit目」が変わってしまった場合、Parity検査ビットは「1,2」の結果が変わります。つまり1bitのエラーならば問題なく検出/訂正できます。
Parity[2]=[1]^[2]^[3]...
Parity[1]=[0]^[2]^[3]...
Parity[0]=[0]^[1]^[3]... -
次にデータの「0bit目と2bit目」が変わった場合を考えると
Parity[2]=[1]^[2]^[3]...
Parity[1]=[0]^[2]^[3]...
Parity[0]=[0]^[1]^[3]...
- このように、Paryty[1]に対して[0]と[2]の2bit分のデータが反転しているため、Parityエラーは検出されません。これよりParity[0][2]の検出結果として、データの「1bit目」が訂正対象になりますが、これは誤判定になります。つまり1bitのエラー訂正はできても、2bitのエラー検出はできない状態です。
-
この2bitのエラー検出対策ですが、非常に簡単です。全データのParityを見る検査bitを追加すれば良いのです。追加後の表が下記になります。単にデータの全bitをEORした結果を持たせるParity[5]が追加されています。
表.SECDEDハミング符号表(16+6bit)
- もしデータのエラーが2個のbitで発生している場合、Parity[5]は元の値と一致します。Paryty[0]〜[4]のどこかでParityエラーが発生しても、Parity[5]がエラーしていない場合は、ダブルエラー検出で訂正不能という判断をすることができます。
- 気付くと16bitのデータに対してParity検査用6bitを追加することでSECDED動作が可能となるEncode/Decode表ができあがってしまいました。実はこれがハミング符号です。データ部の0〜15に対しては、Parity検査の割当がユニークになれば良いので、上記表は組み合わせの一つでしかありません。端的に言えば表のデータbitを表す青背景の数字は位置が入れ替わっても全く問題ありません。できあがった表に合わせて回路(単なるEORの割り振り)を組むだけです。
-
ここでもう一度、ハミング符号表の作り方を整理します。以下の手順で何bitのデータに対しても作成できます。全く数学の話はありません。レシピですね。
- 「1」から初めてデータ幅分を表すのに何bit必要か(SEC Parity bit)考える。
- データ幅+SEC Parity Bitの2進表を作成する。スタートは「1」から。
- 列の中で1個だけ「1」になっている列を寄せて整理する。
- データ全bitを見るParity Bitを追加する。
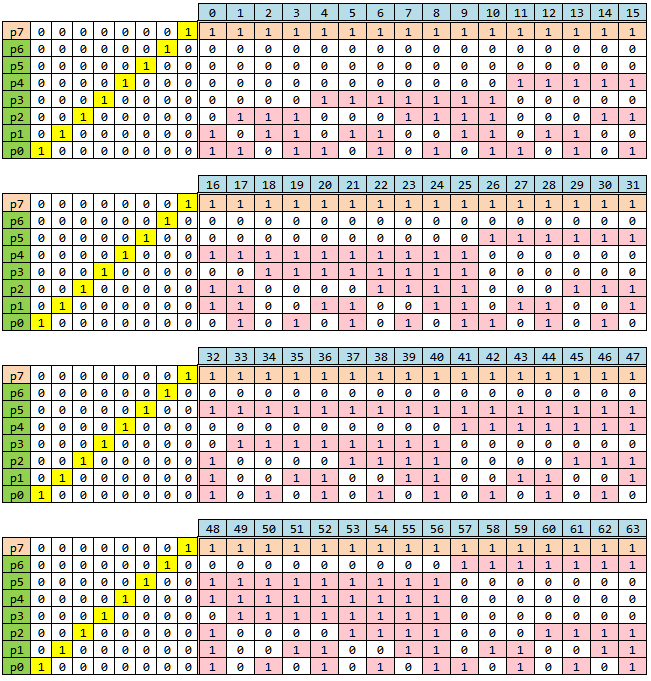
- 現実的には、32bit及び64bitデータへのハミング符号表を必要とするケースが多いので、この手順で作った64bit版符号表を示します。16bitずつ4段に分かれています。尚、下記表は「j_xapp645.pdf」の結果と同じ(*3)になっています。
表.SECDEDハミング符号表(64+8bit)
- ハミング符号表ができたところで、SRAMにECCエンコーダとデコーダを接続してSimulation検証するところまでやりたかったのですが、時間切れとなりました。次回、実際に回路を組んで、Sim検証してみたいと思います。
-
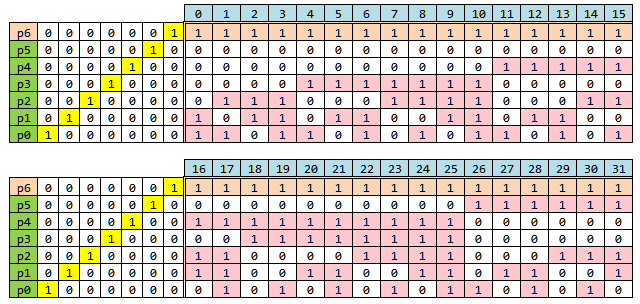
2015/11/8追記:章題には「32bitと64bit...」と書いているのに32bitの表を忘れていました。すみません。
表.SECDEDハミング符号表(32+7bit)
- FPGAメーカ独自のマクロ機能やIPを使用することは、どんどん囲い込まれて抜け出せなくなるのと同義です。常に将来を含めた開発コストに見合うかどうか判断は必要だと考えています。
- ECC云々以前に製品/ビジネスとしては、こちらがかなり問題。SRAM搭載量が、使用するFPGAのシリーズや、ASICのチップ面積を決めるので、量産時のコストに跳ね返ってきます。
- 手順の答え合わせをすることができました。
2015/11/08 : 32bit ハミング符号表追加
Copyright(C) 2015 Altmo
本HPについて
本HPについて