プラネタリーギアセット
2018/08/01
[Prev] [Next] [Top] , Car [Prev] [Next]
プラネタリーギアセットはステップATの中枢部品
  • 前回のCarカテゴリレポートでオートマチックトランスミッションの種類について説明しました。その中でも変速の仕組みが理解し難いのはステップATでしょう。理解の難易度が高い理由は、ステップATが複数のプラネタリーギアセットを使用していることと、そのプラネタリーギアの動きを直感的に理解できないからだと考えています。


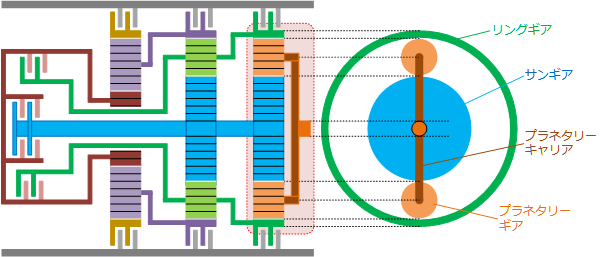
    Figure 1 : ステップATとプラネタリーギアセット

  • そこで今回はステップATを理解する準備編としてプラネタリーギアセットに着目し、その回転数について直感的に理解できるようにしたいと思います。

重要なのは「コロの原理」
  • まず一度プラネタリーギアのことを忘れて「コロの原理」について話をしたいと思います。Figure 2 は ボールを上下から板で挟んでいる状態を示しています(*1)。この板が上下とも同じ速度で動いたら、ボールは全く転がらずに一緒に移動します。板で挟んで運んでいるだけなので、これは特に問題なくわかるでしょう。

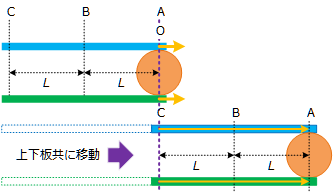
    Figure 2 : 上下板共に移動したときのボールの動き

  • 次は、下の板を固定して上の板だけを動かした場合です。ボールの頂点を板が通り過ぎた分ボールが転がるので、ボールの移動は上の板が移動した距離の半分になります。これがコロの原理です。

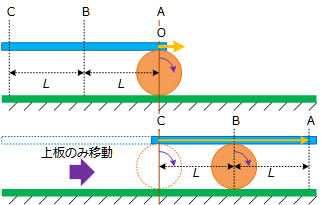
    Figure 3 : 上板だけ移動したときのボールの動き

  • この「ボールの移動は板より少ない」というキーワード/感覚を頭に焼き付けて下さい。ピンと来なければ、実際に丸ボールペンの上に定規を乗せて、その目盛りを見ながら定規の移動距離と転がったペンの移動距離を確認するといった実験をすると、飲み込みやすくなると思います。

そして上下板を丸めるとプラネタリーギアセットが
  • それでは真ん中にボールを挟んだまま、上下の板を丸めてリングにしてみましょう。気付くとプラネタリーギアセットができています。

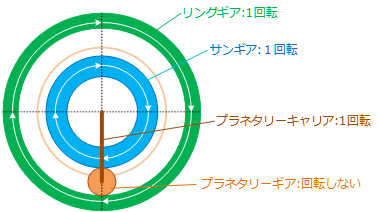
    Figure 4 : リングギア/サンギアとも等速回転する場合

  • Figure 4 はリングギアとサンギアが同じ速度で回転するケースを示しています。ボールを上下板で挟んだ Figure 2 の場合と同じです。

  • リングギア/サンギアが同じ速度で回転すると、プラネタリーギアは転がらずに、プラネタリーキャリアがリング/サンギアと一緒に回転します。プラネタリーギアセット全体を糊付けして回転させるイメージです。

リングギアを固定:プラネタリーキャリアはサンギアより遅く回る
  • 次にリングギアを固定してサンギアだけ回転させるケースを考えてみます。リングギアが止まっているため、サンギアがプラネタリーギアの頂点を通り過ぎるとプラネタリーギアが回転し、静止しているリングギアの上を転がっていきます。Figure 5はその様子を示しています。

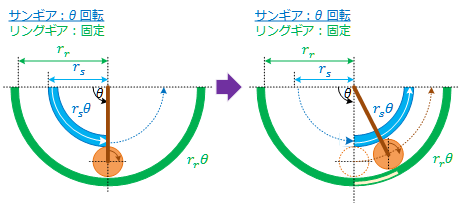
    Figure 5 : リングギア固定、サンギアのみ回転

  • つまりサンギアを入力とした場合、プラネタリーキャリアは減速回転します。プラネタリーキャリアを入力とした場合、サンギアは増速回転します。この仕組を組み合わせて増減速を行っています。

リングギアを固定:プラネタリーキャリアの回転量は?
  • では実際どの程度の回転数になるのか考えてみましょう。Figure 6 の上左側は、プラネタリーキャリアを固定した状態で、サンギアを1回転させている図です。リングギアが逆方向に $r_{s}/r_{r}$ 回転します。これは円周比もしくはギア数比です。


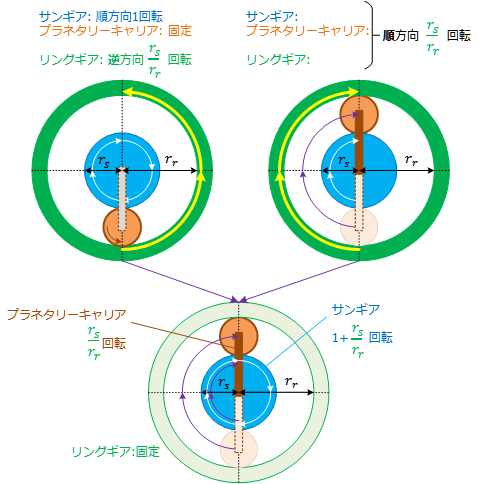
    Figure 6 : リングギア固定時のサンギア/プラネタリーキャリア回転数

  • このときリングギアを固定するとは、リングギアが逆回転した分を戻すことと同じです。そこで今度は全体を$r_{s}/r_{r}$回転させたのが、Figure 6の上右側です。

  • つまり、Figure 6の上右側と上左側を重ね合わせれば、リングギアが0回転になる各ギアの回転比率が求められます。
    • リングギアの回転が0になる条件
        サンギア回転数$\displaystyle =1+\frac{r_{s}}{r_{r}}$
        プラネタリーキャリア回転数$\displaystyle =\frac{r_{s}}{r_{r}}$
    • 上記より、リングギア固定時のサンギア1回転に対するプラネタリーキャリアの回転数は式(1)となります。
        回転比$\displaystyle =\frac{r_{s}/r_{r}}{\left( 1+r_{s}/r_{r} \right)}=\frac{r_{s}}{r_{s}+r_{r}}$　　(1)

  • 具体例として、リングギアとサンギアの半径また歯数比率が $r_{r}:r_{s}=2:1$ のとき、プラネタリーキャリアはサンギアの $1/(1+2)=1/3$ で回転することになります。

サンギアを固定:プラネタリーキャリアの回転量は?
  • サンギアを固定してリングギアだけ回転させるケースですが、これは
    • サンギア/リングギア/プラネタリーキャリア全体を1回転させた後
    • サンギアだけを逆に1回転させると
    サンギア固定と同じ状態になります。

  • サンギアのみ回転させたときのプラネタリーキャリア回転比率は式(1)でわかっているので、サンギア固定でリングギアを1回転させたときの、プラネタリーキャリア回転比は
      回転比$\displaystyle =1-\frac{r_{s}}{r_{r}+r_{s}}=\frac{r_{r}}{r_{r}+r_{s}}$　　(2)
    になります。

  • 具体例として、リングギアとサンギアの半径また歯数比率が $r_{r}:r_{s}=2:1$ のとき、プラネタリーキャリアはリングギアの $2/(1+2)=2/3$ で回転することになります。

サンギアとリングギアが異なる回転をしている場合
  • ここまでに見てきた各ケースの回転数組み合わせをまとめてみます。$r_{r}$ はリングギアの半径又は歯数、$r_{s}$ はサンギアの半径又は歯数です。
    回転ケース リング/サンギア等速 リングギア固定 サンギア固定
    サンギア回転数 $N$ $N$ $0$
    リングギア回転数 $N$ $0$ $N$
    プラネタリーキャリア回転数 $N$ $\displaystyle N\left(\frac{r_{s}}{r_{r}+r_{s}}\right)$ $\displaystyle N\left(\frac{r_{r}}{r_{r}+r_{s}}\right)$

  • リングギアとサンギアが異なる回転数を持つ場合も、上記表の組み合わせとして表現することができます。

  • 例えばリングギアの回転数 $N$ に対し、サンギアが3倍の回転数 $3N$ をもつケースを考えてみます。サンギアがリングギアに対して3倍の回転数を持つとは
    • まずは、リングギアとサンギアが等速で「$N$ 回転」する
    • その後、リングギア固定状態にてサンギアが追加で「$2N$ 回転」する
    と言い換えることができます。

  • すると上の表からリングギアの回転$N$ に対し、プラネタリーキャリアの回転が

      リング:サンギア等速$N$ 回転 + リング固定:サンギア$2N$ 回転
      $\displaystyle = N+2N\left(\frac{r_{s}}{r_{r}+r_{s}}\right)=N\left(1+\frac{2r_{s}}{r_{r}+r_{s}}\right)$

    になることがわかります。そのイメージを Figure 7 に示します。

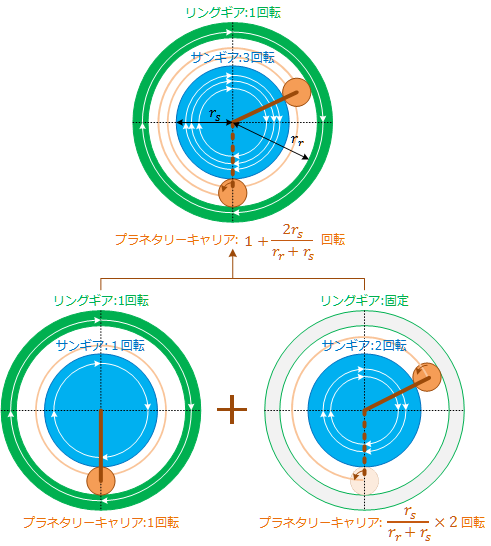
    Figure 7 : 等速回転とサン/リングギア固定回転の組み合わせによる表現

次回は
  • どうでしょうか。今回の説明をまとめると
    • プラネタリーキャリア出力時は、サンギア/リングギア入力に対して減速する
    • サンギア/リングギア出力時は、プラネタリーキャリア入力に対して増速する
    • サンギア/リングギア任意回転時は、全ギア等速/リングギア固定/サンギア固定回転を組み合わせる
    という内容になります。

  • プラネタリーギアセットの扱いについて少しすっきりしたところで、次回はステップATの変速方法を説明したいと思います。
Notes
  • Figure 1 と Figure 2の色付けには相関があります。
2018/07/29 : 初版
2018/08/01 : 計算式誤り訂正,数式表現変更
Copyright(C) 2018 Altmo
本HPについて
[Prev] [Next] [Top] , Car [Prev] [Next]