OPアンプによるアナログ回路(1)

OPアンプによるアナログ回路(1)
2022/12/12

[Prev] [Next] [Top] , Analog Design ~~[Prev]~~ [Next]

アナログ信号の操作/演算はOPアンプを使うことがほとんど

アナログ回路の動作を理解するには、そこで使用されている素子/コンポーネントと、それらを使用した回路ブロックの機能を見ます。ですがトランジスタを用いたアナログ回路の場合、動作点やパラメータなど考慮する点が多く、回路の動作を理解するだけでも大変です。

理解が大変ということは設計も大変なため、現実的なアナログ回路設計、特にアナログ信号の処理/演算部ではOPアンプ(Operational Amplifier)が多用されます。

なぜOPアンプが多用されるのか、それは「OPアンプはコンポーネントの外側にあるフィードバックパスで制御する」からです。フィードバック/帰還パスに置く抵抗の値で増幅度を設計できてしまうのです。

しかしOPアンプの中の話は別レポートとします。今回は「OPアンプを使った回路を読む」ことを目的に、線形動作するOPアンプ回路の代表例を見ていきたいと思います。

仮想短絡がOPアンプ回路理解のポイント

OPアンプは単独で動かすとコンパレータとして動作します。出力が+側電源(Vcc)/-側電源(-Vee)のどちらか(*1)になります。この出力をフィードバック/帰還で制御するのがOPアンプの使い方です。

コンパレータ...入力差が小さくても「+端子 > -端子」なら出力はVcc、「+端子 < -端子」なら出力は-Vee...OPアンプ自身の増幅度は$\infty$であると言えます。

すると、出力をある値に制御するため帰還パスを入力に接続した場合「+端子と-端子の電位差 $\simeq 0$」であると見なすことができます。増幅度$\infty$ですから$0$ではない値が入ったら発散しちゃいますからね。そうなるように帰還されているということです。この「+端子と-端子の電位差 $\simeq 0$」のことを仮想短絡(Virtual Short)と呼びます。

本当にショートしているのではなく、帰還パス接続時に、+端子(非反転入力)と-端子(反転入力)の電位差が$0$と見なせることを指すため「仮想」という言葉がつきます。非反転/反転入力端子間インピーダンスは短絡どころか非常に高い($\infty$)です。

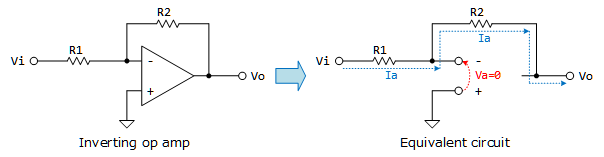
反転増幅回路

Figure 1の左側が反転増幅回路、右側が仮想短絡を適用した等価回路です。ここまで簡単だと回路理論云々はあまり考えなくても良いですね。オームの法則理解だけで充分。

さて、回路解析ですが非反転入力端子が$0V$のため、反転入力端子も$V_{a}=0V$になっていると見なせます。すると、抵抗$R_{1}$を流れる電流$I_{a}$は下記です。 \[I_{a} = \frac{V_{i}-V_{a}}{R_{1}} = \frac{V_{i}}{R_{1}}\]
そして$V_{a}$と$V_{o}$の関係から、反転増幅度が$R_{1}$と$R_{2}$で決まることがわかります。 \[V_{a}-V_{o} = R_{2}I_{a}　→　V_{o} = -V_{i}\frac{R_{2}}{R_{1}}\]
こんな感じで「さっくり」とわかります。引き続き他の回路も見てみましょう。

非反転増幅回路 / ボルテージフォロワ

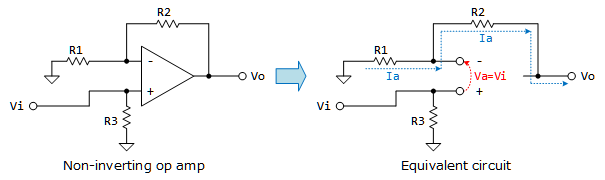
$R_{3}$は前段出力に対する、信号$V_{i}$の入力インピーダンスとなりますが、回路の増幅度計算には絡みません。 \[0-V_{a} = R_{1}I_{a}　→　I_{a}=-\frac{V_{i}}{R_{1}}\] \[V_{a}-V_{o}=R_{2}I_{a}　→　V_{o}=V_{i}-R_{2}I_{a}=V_{i}\left(1+\frac{R_{2}}{R_{1}}\right)\]
さて非反転増幅回路にて$R_{2}=0$(ショート)または$R_{1}=\infty$(オープン)の場合、増幅度は$1$になりますね。この回路はボルテージフォロワ(Voltage follwer)と呼ばれます。前段の出力インピーダンスが大きい場合など、回路を分離する目的で使用します。

Figure 3: ボルテージフォロワ

加算回路

次は加算回路(Adder)です。オペレーショナル(演算)アンプ感がでてきました。ですが、解析としては帰還パスの電流$I_{a}$が、入力パスの電流$I_{1}, I_{2}, I_{3}$の合計であることを意識するぐらいです。

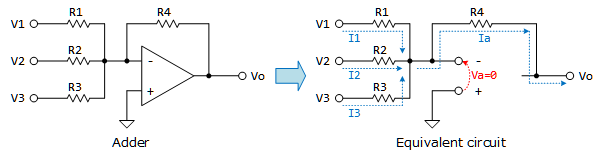
Figure 4: 加算回路
\[V_{1}-V_{a} = R_{1}I_{1}　→　I_{1} = \frac{V_{1}}{R_{1}}\] \[V_{2}-V_{a} = R_{2}I_{2}　→　I_{2} = \frac{V_{2}}{R_{2}}\] \[V_{3}-V_{a} = R_{3}I_{3}　→　I_{3} = \frac{V_{3}}{R_{3}}\] \[I_{a} = I_{1} + I_{2} + I_{3} = \frac{V_{1}}{R_{1}} + \frac{V_{2}}{R_{2}} + \frac{V_{3}}{R_{3}}\] \[V_{a}-V_{o} = R_{4}I_{a}　→　V_{o}=-R_{4}\left(\frac{V_{1}}{R_{1}} + \frac{V_{2}}{R_{2}} + \frac{V_{3}}{R_{3}}\right)\]

差動増幅回路

演算を行うもう一つの回路例は差動増幅回路(Differential amplifier)です。非反転入力への電圧$V_{ip}$から仮想短絡を利用して回路の動作を解析します。

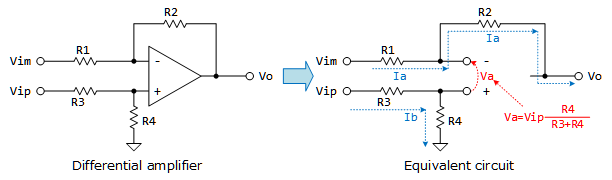
Figure 5: 差動増幅回路
\[V_{ip}=(R_{3}+R_{4})I_{b}　→　I_{b}=\frac{V_{ip}}{R_{3}+R_{4}}\] \[V_{ip}-V_{a}=R_{3}I_{b}　→　V_{a}=V_{ip}-R_{3}I_{b}=V_{ip}\frac{R_{4}}{R_{3}+R_{4}}\] \[V_{im}-V_{a}=R_{1}I_{a}　→　I_{a}=\frac{V_{im}-V_{a}}{R_{1}}=\frac{1}{R_{1}}\left(V_{im}-V_{ip}\frac{R_{4}}{R_{3}+R_{4}}\right)\] \[V_{o}=V_{a}-R_{2}I_{a}\] \[= V_{ip}\frac{R_{4}}{R_{3}+R_{4}} - \frac{R_{2}}{R_{1}}\left(V_{im}-V_{ip}\frac{R_{4}}{R_{3}+R_{4}}\right)\] \[= V_{ip}\left(\frac{R_{4}}{R_{3}+R_{4}}\right)\left(\frac{R_{1}+R_{2}}{R_{1}}\right)-V_{im}\frac{R_{2}}{R_{1}}\]
少し面倒な感じになりました。ここで条件を加えて$R_{1}=R_{3}$, $R_{2}=R_{4}$とすれば、わかりやすくなります。
\[V_{o}=V_{ip}\left(\frac{R_{2}}{R_{1}+R_{2}}\right)\left(\frac{R_{1}+R_{2}}{R_{1}}\right)-V_{im}\frac{R_{2}}{R_{1}}\] \[=(V_{ip}-V_{im})\frac{R_{2}}{R_{1}}\]
ですが、上記は2本の入力信号に対して異なる入力インピーダンスを持つ回路になっているため、実際に差動増幅回路として使うには更に工夫が必要です。こういった細かい考慮については別レポートとします。

インピーダンス整合

高入力インピーダンス/低出力インピーダンスであることを利用し、容易にインピーダンスを整合することができます。例えば映像信号の場合、$75\Omega$の特性インピーダンスを持ちますが、下図のように、出力$V_{f}$に$R_{o}=75\Omega$を接続することで、出力インピーダンスを決めることができます。

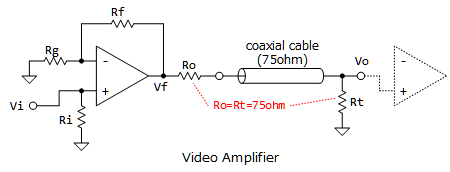
Figure 6: インピーダンス整合

そして次段の入力も$R_{t}=75\Omega$で終端することにより整合を取ることができます。この場合取り出す電圧は、出力$V_{f}$の半分になりますが、次段の増幅回路で2倍することにより出力レベルが戻ります。例えば上図の回路では$R_{g}=R_{f}$とすれば、$V_{f}$は$V_{i}$の2倍として出力されます。

次回へ続きます

Notes

2022-12-12: 初版
2022-12-17: 差動増幅回路を追記

[Prev] [Next] [Top] , Analog Design ~~[Prev]~~ [Next]