2023/01/14
- 前回のレポートで使い方だけ示した等価電圧源の定理(テブナンの定理)ですが、この証明には重ね合わせの理を使用します。
- この前提になっている重ね合わせの理を直感的に理解できていないと、等価電圧源の定理について証明を見てもモヤモヤするでしょう。ですが大抵の場合、重ね合わせの理についての説明は別の場/割愛になっています(*1)。
- 例えば「重ね合わせの理は、線形性の本質の現れであって、証明すべきものではない」といった説明です。線形性の意味を理解できていればシンプルで適切な説明ですが、授業や講義で聞いている際は大抵の人が「線形性...って何だっけ?」と思っているはずです。
- 「あれ?」と思い始めた頃には話が進んでしまい、モヤモヤした状態で次の説明...等価電源の定理を聞くことになります。そしてピンと来ない原理を使って証明した定理は当然飲み込めない(*2)ため、応用できない知識になってしまいます...。
- そんな理由で、まずは線形性から見ていきましょう。
線形性とは
- ある入力$x,y$に対し、ある作用や演算$f$の結果が下記の性質を持つとき、$f$は線形の系であると言います。
$f(x+y)=f(x)+f(y)$ : 加法性
$f(ax)=af(x)$ : 斉次/同次性 - 特に加法性を図にすると下記です。
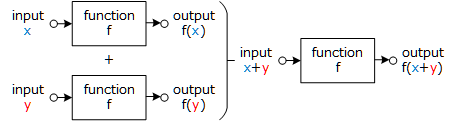
Figure 1: 線形の性質-加法性 - 加法性:$f(x+y)=f(x)+f(y)$ を見て下さい...そのまま「重ね合わせの理」です。つまり「線形の系が持つ加法性を解析に利用すること」を重ね合わせの理と呼んでいるのです(*3)。
電気回路は線形の系なのか
- 要は線形の性質を使って解析するのだなとわかったところで、次の疑問は「電気回路は線形の系なのか?」でしょう。
- 結論から言うと線形です。ただし「FET/トランジスタ/ダイオードといった能動素子を非飽和領域で使うことが条件」です。
- 例えばTr出力が飽和しない領域で小信号増幅する回路は線形回路です。よってアナログ系電気回路の多くは線形回路と考えても良いです。しかしコンパレータのように出力が1/0となるようなFET/Trを飽和領域で使用する回路は非線形に分類されます。
- さて、なぜ通常の電気回路は線形だと言えるのかですが、電気回路の岐路ではオームの法則$(V=ZI)$が成立するからです。電気回路は、これらの岐路を組み合わせた1次式として成立するため線形の系となります。
等価電圧源の定理を証明する
- それでは重ね合わせの理、線形回路の加法性を利用することに心理的抵抗が無くなったところで、等価電圧源の定理を証明してみましょう。何らかの回路(Black Box)において、開放端電圧を$V_{f}$、開放端インピーダンスを$Z_{o}$とします。この回路は「電源電圧$V_{f}$で出力インピーダンス$Z_{o}$の回路に置き換えられる」ことを等価電圧源の定理と呼びます。
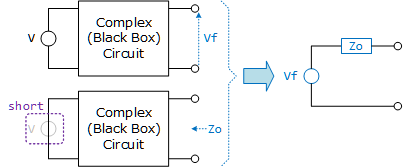
Figure 2: 等価電圧源(テブナン/鳳-テブナン)の定理 - この回路に負荷$Z$を接続したのがFigure 3の回路(a)です。そして、負荷$Z$に対して、正負の$\pm V_{f}$となる電源$V_{1}$と$V_{2}$を追加したのが、Figure 3の回路(b)です。$V_{1}$と$V_{2}$は打ち消し合うため、Figure 3の回路(a)と(b)は同じ回路になります。
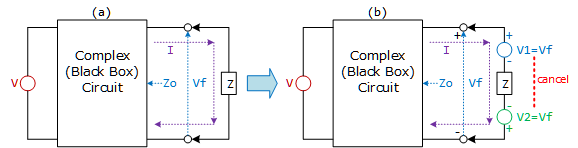
Figure 3: ある回路に$V_{1}$と$V_{2}$を追加した等価な回路 - Figure 3の回路(a)と(b)は等しいので、重ね合わせの理を使って回路(b)を解析すれば回路(a)の挙動も見ることができます。Figure 4は回路(b)を、回路(c)と(d)の重ね合わせとして表現したものです。
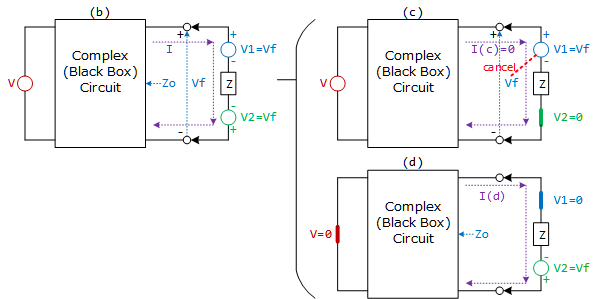
Figure 4: 重ね合わせの理を使用した解析 - 追加電源$V_{2}=0$とした回路(c)では、開放端電圧$V_{f}$と$V_{1}(=V_{f})$は打ち消し合うため、負荷$Z$を流れる電流$I_{(c)}$は$0$になります。次にBlack Box回路の電源$V=0$, 追加電源$V_{1}=0$とした回路(d)ですが、$V_{2}=-V_{f}$, $Z$, $Z_{o}$から電流$I_{(d)}$が決まります。
\[I_{(d)}=\frac{V_{f}}{Z_{o}+Z}\] - すると重ね合わせの理から、回路(b)の状態で負荷$Z$に流れる電流$I$は下記となります。
\[I=I_{(c)}+I_{(d)}=0+I_{(d)}=\frac{V_{f}}{Z_{o}+Z}\] - この結果から回路Black Boxは電源電圧$V_{f}$で出力インピーダンス$Z_{o}$の回路と等価だと言うことができます。これが等価電圧源の定理(テブナンの定理)です。
重ね合わせの理はいろいろ応用できる
- 今回は等価電圧源の定理をモチーフに電気回路に対して重ね合わせの理を使用しましたが、線形の系全てに適用できるため、多く物理事象に重ね合わせの理を利用することができます。
- うーん、ちょっとややこしいなと思ったら、簡単になる組み合わせを考えてみると良いかもしれませんね。
- 本だと割ける紙面に限りがありますからね(良心的表現です)。
- また定理名に人名を適用することで更に意味から遠ざける...わかりにくくなる仕掛け多過ぎ。
- 過去のコンテンツではプラネタリーギアセットの説明にて重ね合わせの理を使っていました。
2023-01-15: 等価電圧源の定理図追加。その他の図に電流記号と電圧cancel記号追加。
Copyright(C) 2023 Altmo
本HPについて
本HPについて